Probability Waves and Complementarity

The acceptance of light as composed of particles (or photons) led to another shocking realization. For example, if light shines on an imperfectly transparent sheet of glass, it may happen that 95% of the light transmits through the glass while 5% is reflected back. This makes perfect sense if light is a wave (the wave simply splits and a smaller wave is reflected back). But if light is considered as a stream of identical particles, then all we can say is that each and every photon arriving at the glass has a 95% chance of being transmitted and a 5% chance of being reflected.

The actual behavior of any individual photon is therefore totally random and unpredictable, not just in practice but even in principle. Although the tossing of a coin, for example, is random in practice, if we knew precisely everything about the force, angle, shape, air currents, etc, we could, in principle, predict the outcome accurately. The behavior of a sub-atomic particle, however, is random on a whole different level, and can never be predicted.

Thus, it is not possible to predict a single definite result for an observation, only a number of different possible outcomes, each with a particular likelihood or probability. Physics had therefore changed overnight from a study of absolute certainty, to one of merely predicting the odds!

The reason we do not see the effects of this on a more macro scale is that everyday objects are composed of billions or trillions of sub-atomic particles. Although the position of each individual particle may be highly uncertain, because there are so many of them acting in unison in an everyday object, the combined probabilities add up to what is, to all intents and purposes, a certainty.

In order to reconcile the wave-like and particle-like behavior of light, its wave-like aspect needs to be able to “inform” its particle-like aspect about how to behave, and vice versa. It was the Austrian physicist Erwin Schrödinger, along with the German Max Born, who first realized this and worked out the mechanism for this information transference in the 1920s, by imagining an abstract mathematical wave called a probability wave (or wave function) which could inform a particle of what to do in different situations. Erwin Schrödinger proposed a ground-breaking wave equation, analogous to the known equations for other wave motions in nature, to describe such a wave. Born further demonstrated that the probability of finding a particle at any point (its "probability density") was related to the square of the height of the probability wave at that point.

(Click for a larger version) Probability density plots of some hydrogen atomic orbitals (Source: Wikipedia: http://en.wikipedia.org/wiki/Wave_function)

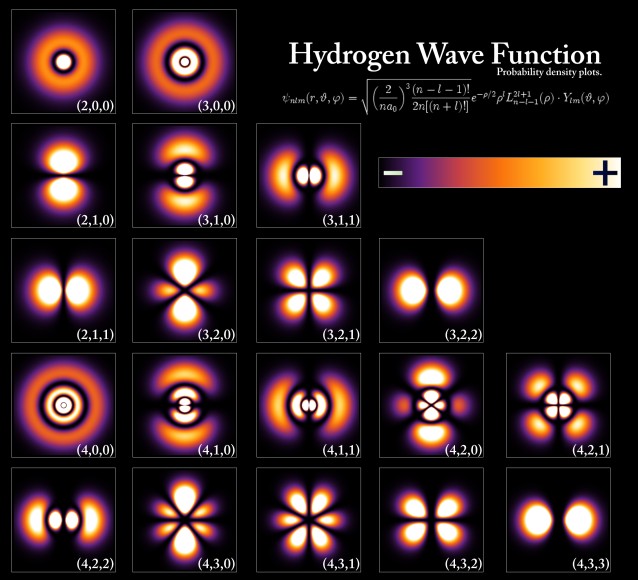
Schrödinger worked out the exact solutions of the wave equation for the hydrogen atom, and the results perfectly agreed with the known energy levels of these atoms. It was soon found that the equation could also be applied to more complicated atoms, and even to particles not bound in atoms at all. In fact, in theory it applies to ALL matter, although massive objects exhibit very small wavelengths, so small that it is rather pointless to think of them in a wave fashion. But for small objects like elementary particles, the wavelength can be observable and significant.

Like light, then, particles are also subject to wave-particle duality: a particle is also a wave, and a wave is also a particle. Using Schrödinger's wave equation, therefore, it became possible to determine the probability of finding a particle at any location in space at any time. This ability to describe reality in the form of waves is at the heart of quantum mechanics. In 1926, Schrödinger published a proof showing that Heisenberg’s matrix mechanics and his own wave mechanics were in fact equivalent, and merely represented different versions of the same theory.

The Danish physicist Niels Bohr, who, along with Heisenberg and Schrödinger, was integrally involved in the early development of quantum mechanics, tried to come to grips with some of the philosophical implications of quantum theory in the early 1920s. He felt that the classical and quantum mechanical models were two complementary ways of dealing with physics, both of which were necessary, an idea he called “complementarity”. This idea of complementarity formed the basis of what became known as the “Copenhagen interpretation” of quantum physics, a deeply divisive idea in the world of physics at the time.

(Click for a larger version) The collapse of a probability wave function (Source: Mukto-Mona: http://www.mukto-mona.com/Special_Event_/ rationalist_day/2005/ quantum_quackery_vic.htm)

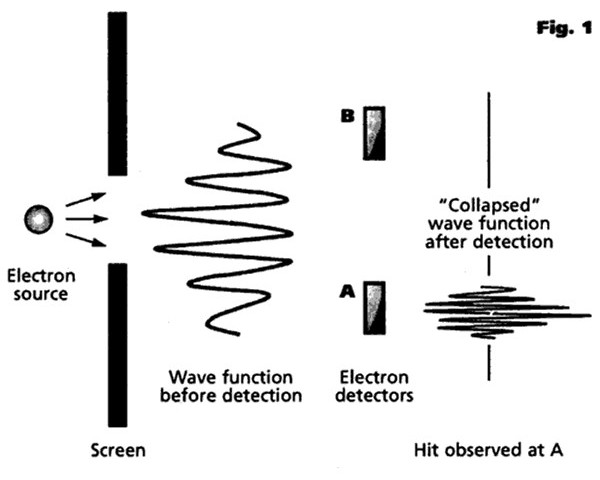
Bohr felt that an experimental observation “collapsed” or “ruptured” the wave function to make its future evolution consistent with what we observe experimentally (an idea that will become very important in our subsequent explanations of quantum effects such as decoherence, entanglement and the uncertainty principle). As soon as a photon, for example, is observed or detected in a particular place, then the probability of its being detected in any other place suddenly becomes zero. Up until that point, the particle's position is inherently uncertain and unpredictable, an uncertainty that only disappears when it is observed and measured. This immediate transition from a multi-faceted potentiality to a single actuality (or, alternatively, from a multi-dimensional reality to a 3-dimensional reality compatible with our own everyday experience) is sometimes referred to as a quantum jump.

However, Bohr also believed that there was no precise way to define the exact point at which such a collapse occurred, and it was therefore necessary to discard the laws governing individual events in favor of a direct statement of the laws governing aggregations. According to this model, there is no deep quantum reality, no actual world of electrons and photons, only a description of the world in these terms, and quantum mechanics merely affords us a formalism that we can use to predict and manipulate events and the properties of matter.

The Copenhagen interpretation, then, is essentially a pragmatic view, effectively saying that it really does not matter exactly what quantum mechanics is all about, the important thing being that it “works” (in the sense that it correlates with reality) in all possible experimental situations, and that no other theory can explain sub-atomic particles in any more detail.

Albert Einstein, whose work had been instrumental in much of the early development of quantum theory, had grave philosophical difficulties with the Copenhagen interpretation, and carried on an extensive correspondence with both Bohr and Heisenberg on the matter, arguing that the physical world must have real properties whether or not one measures them, famously claiming in 1926 that “I, at any rate, am convinced that He [God] does not throw dice". He took particular exception to Bohr’s claim that a complete understanding of reality lies forever beyond the capabilities of rational thought. Both Einstein and Erwin Schrödinger published a number of thought experiments designed to show the limitations of the Copenhagen interpretation and to show that things can exist beyond what is described by quantum mechanics.

Einstein's position was not so much that quantum theory was wrong as that it must be incomplete. He insisted to his dying day that the idea that a particle's position before observation was inherently unknowable (and, particularly, the existence of quantum effects such as entanglement as a result of this) was nonsense and made a mockery of the whole of physics. He was convinced that the positions and quantum states of particles (even supposedly entangled particles) must already have been established before observation. However, the practical impossibility of experimentally proving this argument one way or another made it essentially a matter of philosophy rather than physics.

And so it remained until the experimental work of the American physicist John Clauser and others in the early 1970s, as we will see in the later section on Nonlocality and Entanglement.